Overview

Statistics and probability are important tools for the analysis of data.

 

Basic Statistics

Sample Mean

$$ \bar{x} = \dfrac{1}{n} \sum\limits_{i=1} x_i$$

data <- c(1,2,3,4,5)
mean(data)
sum(data)/length(data)

Sample Variance

$$ s^2 = \dfrac{1}{n-1} \sum\limits_{i=1} (x_i - \bar{x}^2) $$

var(data)
sum( (data - mean(data))^2 ) / (length(data) - 1)

Sample Standard Deviation

$$ s = \sqrt{s^2}$$

sd(data)
sqrt( var(data) )

 

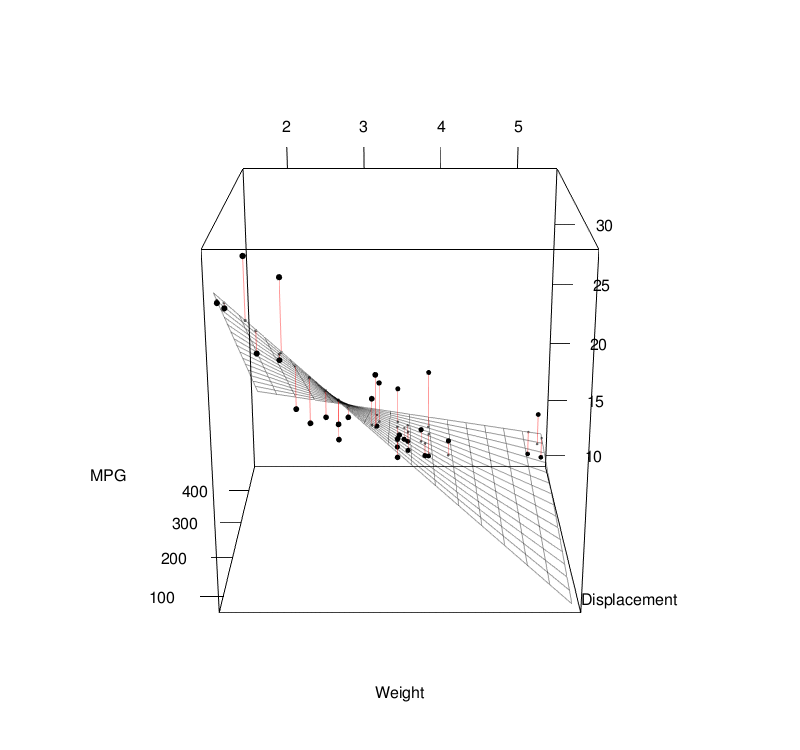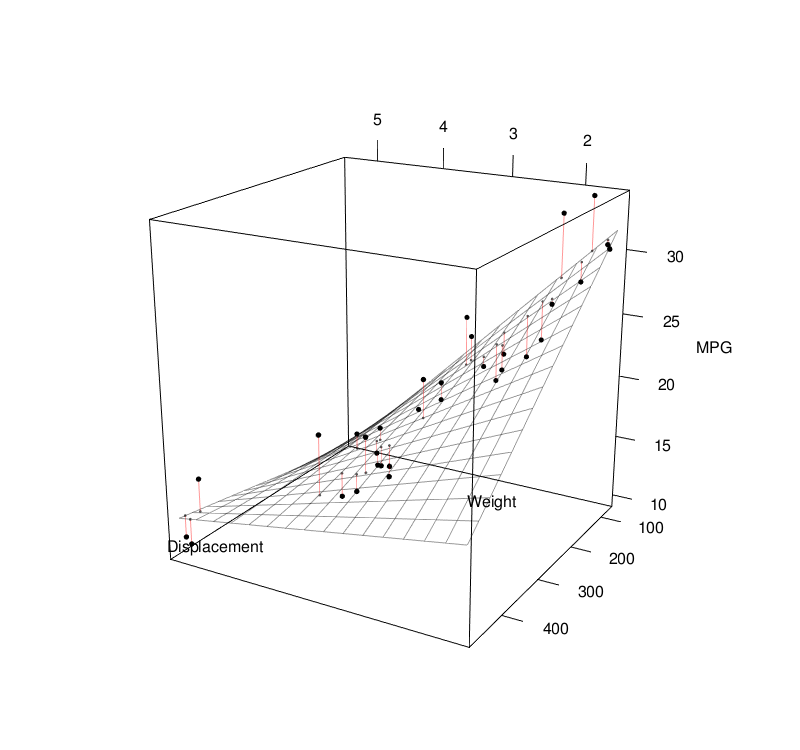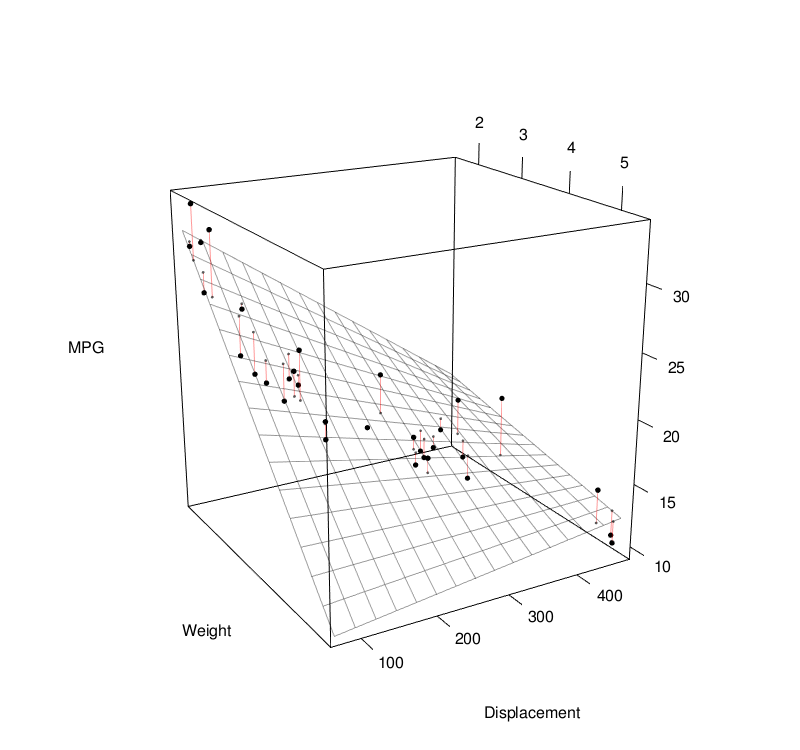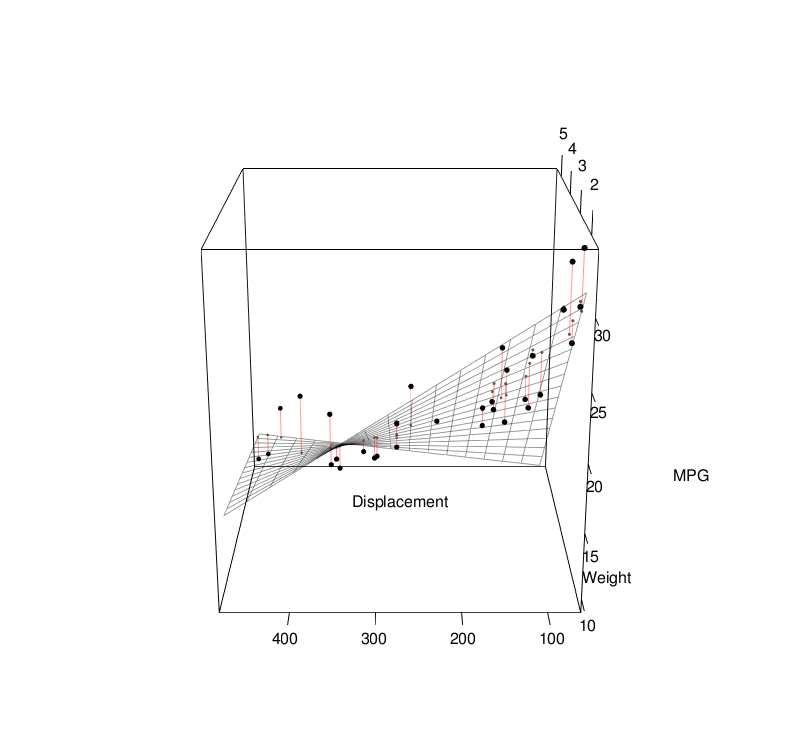
Linear Regression

Linear regression models assume some relationship exists between a response variable ( \(y\) ) and its predictor (or independent) variables ( \(\mathbf{x} \) ). $$ \begin{align} y &= \mathbf{x} \beta + \epsilon \\[1em] &= \beta_0 + \beta_1 x_1 + \beta_2 x_2 + ... + \beta_p x_p + \epsilon \\[1em] \end{align} $$

To estimate the coefficients, we can use the least-squares approach:

$$ \begin{align} \hat{\beta} &= (\mathbf{x}^T \mathbf{x})^{-1} \, \mathbf{x}^T \mathbf{y} \\[1em] &= \beta_0 + \beta_1 x_1 + \beta_2 x_2 + ... + \beta_p x_p + \epsilon \\[1em] \end{align} $$

We can use the following code in R to estimate the coefficients manually.

	betahat <- solve( t(x) %*% x ) %*% t(x) %*% y

Linear Regression Model Predictions

Once we obtain the \( \beta \) weights for our model (either by deriving them or through Gradient Descent), we can have the model estimate/predict values for given input data:

$$\hat{y} = \mathbf{x} \beta$$ $$h_\mathbf{\beta}(\mathbf{x}) = \hat{y} = \mathbf{x}\beta$$

The hypothesis function \( h_\beta(\mathbf{x}) \) (outputs are often denoted as \(\hat{y} \)) accepts some record \(\mathbf{x} = \begin{bmatrix} 1& x_1 & x_2 & ... & x_p \end{bmatrix}\) and multiplies it by the corresponding weights \( \beta = \begin{bmatrix} \beta_0 \\ \beta_1 \\ \beta_2 \\ \vdots \\ \beta_p \end{bmatrix}\).

#****************************************************
#* Define a function named "predict" that serves as
#* the hypothesis function.
#* 
#* @param    w      a vector of weights
#* @param    x      a vector of inputs
#****************************************************

predict <-  function(w,x) {
  result <- x %*% w    # matrix multiplication
  return(result)
}

# Example weights (betas)
w <- c(100, 0.5, 2.0)

# Example input vector
x <- c(1, 30, 2)


# Element-wise multiplication
yhat <- sum(w*x)
print(yhat)

# Matrix multiplication
yhat <- predict(w,x)
print(yhat)

Suppose that we had a dataset with two features, \(\mathbf{x}_1\) and \(\mathbf{x}_2\). We will define the following sample data comprised of two features and four records, giving us the resulting dimensions of \( 4 \times 2\):

$$\mathbf{X} = \begin{bmatrix} 10 & 20 \\ 30 & 40 \\ 50 & 60 \\ 70 & 80 \end{bmatrix}$$

mydata <- c(10, 20, 30, 40, 50, 60, 70, 80)
X <- matrix(data=mydata, nrow = 4, ncol = 2, byrow=TRUE)

Next, we need to add the bias column for our matrix:

$$\mathbf{X} = \begin{bmatrix} 1 & 10 & 20 \\ 1 & 30 & 40 \\ 1 & 50 & 60 \\ 1 & 70 & 80 \end{bmatrix}$$

biasweight <- 1
bias <- replicate(n=4, expr=biasweight)
X <- cbind(bias, X)

We can now predict all \(n\) records in \(\mathbf{X}\) using matrix multiplication as \(\mathbf{X} \times \mathbf{w}\):

yhats <- predict(w,X)